Ex-01
Qual a probabilidade de obtermos 5 “caras”, em cinco
lançamentos sucessivos de uma moeda sem vícios?
Solução
Podemos aplicar o princípio fundamental da contagem:
A probabilidade do evento “cara” ocorrer em 1 lançamento:
p(cara)=1/2; e
Sendo 5 lançamentos, temos que:
Ex-02
Qual é a probabilidade de, em um grupo de 10 pessoas,
escolhidas aleatoriamente, ao menos uma delas ter nascido em julho?
Solução:
O caminho mais fácil é aplicar a probabilidade complementar.
Primeiramente, vamos calcular a probabilidade de nenhuma
das pessoas nascerem em julho e, em seguida, subtraímos o resultado de 1
(é sabido que: duas probabilidades, em
um mesmo universo, são complementares, então, a soma de suas probabilidades é
igual a 1)
A probabilidade de cada uma das
pessoas não ter nascido em julho é 11/12. Como são 10 pessoas, aplicando o
princípio multiplicativo (= princípio fundamental da contagem), temos que:
Portanto, a probabilidade de que
algumas das 10 pessoas ou pelo menos uma delas, ter nascido em julho (o que
se pede no enunciado) é:
Ex-03
(Um problema clássico).
O que é mais provável de ocorrer: obter pelo menos um 6 em 4 lances de
um único dado, ou obter pelo menos um 12 em 24 lances de um par de dados? Considerar que os dados são todos sem
vícios.
Adotar:
Solução:
a) Probabilidade de ocorrer pelo menos um 6 nos 4
lances de um dado é:
b) Probabilidade de ocorrer pelo menos um 12 nos 24
lances de um par de dados é:
Portanto,
a mais provável de ocorrer é um 6 nos 4 lances de um dado.
Ex-04
(Um problema clássico). O problema da coincidência de
aniversários.
Em um grupo de 20 pessoas, determinar a probabilidade de que
duas dessas pessoas, pelo menos, tenham aniversário mesmo dia.
Solução:
Pela aplicação de probabilidade complementar.
Portanto, em primeiro lugar
determinar a probabilidade de que todas 20 pessoas façam aniversários em datas
diferentes, e depois, calcular o que se pede pela probabilidade
complementar.
Para simplificar um pouco, vamos
supor que não exista ano bissexto; então ano de 365 dias.
O número de possibilidades das 20 pessoas terem nascidos em
datas diferentes é:
n(E)=365*364*363*362*361*...*348*347*346
Nota: [365-20+1 = 366 – 20]
O campo amostral (= o universo de todas as possibilidades);
número total de possibilidades das 20 pessoas de fazerem o aniversário é:
n(S)=365*365*365* ... *365*365
= 36520
Logo, a probabilidade das 20 pessoas aniversariarem em datas
distintas é:
Portanto, a probabilidade de, pelo menos, 2 pessoas façam
aniversários no mesmo dia é:
Como curiosidade, vamos fazer uma generalização:
A probabilidade de, em um grupo de k pessoas, encontramos pelo menos duas
com a mesma data de aniversário é dada por:
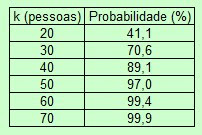
Fazendo os cálculos para k variando
de 20 a
70, temos a seguinte tabela:
Observa-se que em um grupo de 70
pessoas é certo de que duas pessoas nasceram no mesmo dia. Já com 50 pessoas é
quase certo que existem 2 aniversariantes no mesmo dia.
Ex-05
De quantas maneiras 6 pessoas podem sentar-se num banco de 6
lugares de modo que duas delas fiquem sempre juntas, em qualquer ordem?
Solução
Como duas pessoas ficarão sempre juntas, podemos
considerá-las uma única pessoa. Dessa forma temos que:
Permutação de 5 pessoas:
P5 = 5! = 5 * 4 * 3 * 2 * 1 = 120
Sabendo que as duas pessoas podem se sentar de duas
maneiras, teremos:
2 * 120 = 240.
Portanto
as 6 pessoas podem ocupar o banco de 6 lugares, em que 2 fiquem sempre juntas,
de 240 maneiras.
Ex-06 (UNIFOR-CE)
Um casal e seus quatro filhos vão ser colocados lado a lado
para tirar uma foto. Se todos os filhos devem ficar entre os pais, de quantos
modos distintos os seis podem posar para tirar a foto?
Solução
Os pais se posicionam nos extremos, portanto, temos 2
maneiras:
(P_ _ _ _M, ou M_ _ _ _P).
Quanto aos filhos podemos permutar as 4 posições:
4! = 4.3.2.1 = 24 maneiras diferentes:
Portanto,
Temos 2*24
= 48 modos distintos de posar para a foto.
Ex-07 (UFJF-MG)
Newton possui 9 livros distintos, sendo 4 de Geometria, 2 de
Álgebra e 3 de Análise. O número de maneiras pelas quais Newton pode arrumar
esses livros em uma estante, de forma que os livros de mesmo assunto permaneçam
juntos, é:
Solução
Como os livros de mesmo assunto devem ficar juntos, temos:
4 de Geometria → Permutação de 4 → 4! = 4.3.2.1 = 24
2 de Álgebra → Permutação de 2 → 2! = 2.1 = 2
3 de Análise → Permutação de 3 → 3.2.1 = 6
Agora posso permutar os 3 conjuntos de livros, logo
3! = 3.2.1 = 6
Portanto, o número total de arranjar os livros é:
(24*2*6)*6
= 1728
Ex-08 (ITA)
Quantos números de seis algarismos distintos podemos formar,
usando os dígitos 1, 2, 3, 4, 5 e 6, nos quais o 1 e o 2 nunca ocupam posições
adjacentes (juntos), mas o 3 e o 4 sempre ocupam posições adjacentes?
Solução
Como 3 e o 4 estão sempre juntos, podemos considerar como 1
algarismo, porém, podem ser 34 ou 43 (portanto, 2 maneiras).
Podemos permutar os 5 algarismos, logo:
2*5! = 2*(5.4.3.2.1) = 2*120
= 240 números
Agora vamos calcular os arranjos possíveis para 1 e o 2 juntos
(12 ou 21) e 3 e o 4 juntos (34 ou 43):
Portanto, temos:
4!*2*2 = 4.3.2.1.2.2 = 96 números
Como 1 e o 2 não podem nunca estar juntos, tem-se:
3 e o 4 juntos e 1 e o 2 nunca juntos.
240 –
96 = 144 números
Ex-09
Quantos pratos diferentes podem ser solicitados por um
cliente de restaurante, tendo disponível 3 tipos de arroz, 2 de feijão, 3 de
macarrão, 2 tipos de cervejas e 3 tipos de refrigerante, sendo que o cliente
não pode pedir cerveja e refrigerante ao mesmo tempo, e que ele obrigatoriamente
tenha de escolher uma opção de cada alimento?
Solução
Número total de pratos diferentes: 3*2*3
= 18
A escolha de bebida: cerveja ou refrigerante → (2 + 3) = 5
Logo, o
número total de prato com bebida diferentes possíveis é: 18*5 = 90
Ex-10
Para montar um computador, temos 3 tipos de monitores
diferentes, 4 tipos de teclados, 2 tipos de impressora e 3 tipos de CPU. Pergunta-se: quantas configurações diferentes
podemos montar?
Solução
Aplicação do princípio fundamental da contagem. Portanto, basta multiplicar o números de
opções entre as escolhas que podemos fazer.
3 * 4 * 2 * 3 = 72
Resposta: tem-se 72 possibilidades de
configurações diferentes.








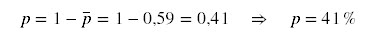

Nenhum comentário:
Postar um comentário