Ex-01
Uma bola será retirada
de uma sacola contendo 5 bolas verdes e 7 bolas amarelas. Qual a probabilidade
desta bola ser verde?
Solução:
Neste exercício o espaço amostral possui 12 elementos, que é o número total de bolas,
portanto a probabilidade de ser retirada uma bola verde está na razão de 5 para 12.
Portanto,
Sendo S o espaço amostral e E o evento da retirada de uma bola verde,
matematicamente podemos representar a resolução assim:
Resposta:
A probabilidade de ser verde é 42%
Ex-02
Uma urna possui 6
bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com
reposição, calcule as probabilidades seguintes:
a) Sair bola azul.
b) Sair bola vermelha.
c) Sair bola amarela
Solução:
O espaço amostral é 20 elementos
que corresponde à total de bolas.
a) P(azul) = 6/20 = 0,30 = 30%
b) P(vermelha) = 10/20 = 0,50 = 50%
c) P(amarela) = 4/20 = 0,20 = 20%
Resposta:
As
probabilidades são: de sair azul é 30%;
de sair vermelha é 50% e de sair amarela é 20%
Ex-03
Considere o
lançamento de um dado. Calcule a probabilidade de:
a) Sair o número 3.
b) Sair um número par.
c) Sair um múltiplo de 3.
Solução:
Espaço amostra neste
problema: 6 possibilidades.
a) Temos: S = {1, 2, 3, 4, 5, 6} → n(S) = 6; n(A) = 1
Portanto,
P(A) = n(A)/n(S) = 1/6 ≈ 0,17 = 17%
b) Temos: n(S) = 6; A = {2, 4, 6} → n(A) = 3
Portanto,
P(A) = n(A)/n(S) = 3/6 = 0,50 = 50%
c) Temos: n(S) = 6; A = {3, 6} → n(A) = 2
Portanto,
P(A) = n(A)/n(S) = 2/6 =1/3 ≈ 0,33 = 33%
Resposta:
As
probabilidades são: de sair número 3 é 17%; de sair número par é 50% e de sair
múltiplo de três é 33%
Ex-04
Ao se retirar uma
carta do baralho, qual a probabilidade de ocorrer uma dama?
Solução:
Um baralho tem 52 cartas,
portanto, o espaço amostral é de 52 elementos: n(S) = 52
O evento desejado (uma dama)
possui 4 elementos (ouros, copas, paus, espadas), portanto, n(A) = 4.
Logo,
P(A) = n(A)/n(S) = 4/52 =
1/13 ≈ 0,077 → P(A) = 7,7%
Resposta:
A
probabilidade de ocorrer uma dama é 7,7%
Ex-05
Três moedas são lançadas ao mesmo tempo. Qual é a
probabilidade de as três moedas caírem com a mesma face para cima?
Solução:
Através do princípio fundamental da contagem podemos determinar o número total de
agrupamentos ao lançarmos três moedas.
Como cada moeda pode produzir dois
resultados distintos, três moedas irão produzir 2 . 2 . 2 resultados distintos, ou seja, poderão
produzir 8 resultados distintos. Este é o nosso
espaço amostral.
Dentre as 8 possibilidades do espaço amostral, o
evento que representa todas as moedas com a mesma face para cima possui apenas 2 possibilidades, ou tudo cara ou tudo
coroa, então a probabilidade será dada por:
Resposta:
A probabilidade
de 3 moedas caírem com a mesma face para cima é 25%.
Ex-06 (FUVEST)
Uma urna contém 3
bolas: uma verde, uma azul e uma branca. Tira-se uma bola ao acaso, registra-se
a cor e coloca-se a bola de volta a urna. Repete-se essa experiência mais duas
vezes. Qual a probabilidade de serem registradas três cores distintas?
Solução:
1 verde, 1 azul, 1 branca
(experiência com reposição para 3 retiradas), logo
n(S) = 3.3.3 = 27
Evento A: saírem três cores
diferentes = permutação de 3 = 3! = 3*2*1 = 6
P(A) = 6/27 = 2/9 ≈ 0,22 = 22%
Resposta:
A
probabilidade de serem três cores distintas é 22%
Ex-07
Um casal pretende ter filhos. Sabe-se que a cada mês
a probabilidade da mulher engravidar é de 20%. Qual é a probabilidade dela vir
a engravidar somente no quarto mês de tentativas?
Solução:
Sabemos que a probabilidade da mulher
engravidar em um mês é de 20%, que na forma decimal é igual a 0,2. A probabilidade dela não conseguir
engravidar é igual a 1 - 0,2, ou seja, é igual a 0,8.
Este exercício trata de eventos
consecutivos e independentes (pelo menos enquanto ela não engravida), então a
probabilidade de que todos eles ocorram, é dado pelo produto de todas as
probabilidades individuais. Como a mulher só deve engravidar no quarto mês,
então a probabilidade dos três meses anteriores deve ser igual à probabilidade
dela não engravidar no mês, logo:
Resposta:
A
probabilidade de engravidar no 4º mês é 10,24%
Ex-08
Um credor está à sua procura. A probabilidade dele
encontrá-lo em casa é 0,4. Se ele fizer 5 tentativas, qual a probabilidade do
credor lhe encontrar uma vez em casa?
Solução:
Ou
o credor vai a sua casa e o encontra, ou ele vai e não o encontra, como em cada
tentativa estamos tratando de um sucesso ou de um fracasso e não há outra possibilidade, além do fato de a
probabilidade ser a mesma em todas as tentativas, vamos resolver o problema
utilizando o termo geral do Binômio de Newton:
n é o número de tentativas de encontrá-lo, portanto n = 5;
k é o número de tentativas nas quais ele o encontra,
portanto k = 1;
p é a probabilidade de você ser encontrado, logo p = 0,4;
q é a probabilidade de você não ser encontrado,
logo q = 1 - 0,4, ou seja, q = 0,6;
Substituindo
tais valores na fórmula temos:
Ex-09
Em uma caixa há 2 fichas
amarelas, 5 fichas azuis e 7 fichas verdes. Se retirarmos uma única ficha, qual
a probabilidade dela ser verde ou amarela?
Solução:
Sabemos que a probabilidade da união de dois eventos pode ser calculada através
da fórmula
e no caso da intersecção dos eventos ser vazia, isto
é, não haver elementos em comum aos dois eventos, podemos simplesmente utilizar
Ao somarmos a quantidade de fichas obtemos a quantidade 14. Esta quantidade é o
número total de elementos do espaço amostral.
Neste exercício os eventos obter ficha verde e obter ficha amarela são mutuamente
exclusivos, pois a ocorrência de um impede a ocorrência do outro, não há
elementos que fazem parte dos dois eventos. Não há bolas verdes que são também
amarelas. Neste caso então podemos utilizar a fórmula:
Note que esta
fórmula nada mais é que a soma da probabilidade de cada um dos eventos.
O evento de se obter ficha verde possui 7 elementos e o espaço amostral possui 14 elementos, que é o número total de fichas, então a probabilidade do
evento obter ficha verde ocorrer é igual a 7/14:
Analogamente, a probabilidade do evento obter ficha amarela, que possui 2 elementos, é igual a 2/14:
Observe que poderíamos ter simplificado
as probabilidades, quando então 7/14 passaria
a 1/2 e 2/14 a 1/7, no entanto isto não foi feito,
já que para somarmos as duas probabilidades precisamos que elas tenham um
denominador comum:
Este exercício foi resolvido através da
fórmula da probabilidade da
união de dois eventos para
que você tivesse um exemplo da utilização da mesma e pudesse aprender quando
utilizá-la, mas se você prestar atenção ao enunciado, poderá ver que poderíamos
tê-lo resolvido de uma outra forma, que em alguns casos pode tornar a resolução
mais rápida.
Vejamos:
Note que a
probabilidade de se obter ficha azul é 5 em 14, ou seja, 5/14. Então a probabilidade de não se obter ficha azul é 9 em 14, pois:
O 1 que aparece na expressão acima se
refere à probabilidade do espaço amostral.
Note que
utilizamos o conceito de evento
complementar, pois se não tivermos uma ficha azul, só poderemos ter uma ficha verde ou uma ficha amarela, pois não há outra opção.
Ex-10 (FUVEST)
Numa urna há 5 bolas brancas, 3 azuis, 4 verdes, 2 amarelas e uma
marrom. Extraindo uma bola ao acaso, a probabilidade de sair uma bola azul ou
amarela é?
Solução:
Espaço
amostral é a soma de todas as bolas: n(S) = 15.
Evento
A: (sai bola azul) → n(A) = 3
Então,
P(A) = n(A)/n(S) = 3/15
Evento
B: (sai bola amarela) → n(B) = 2
Então,
P(B) = n(B)/n(S) = 2/15
Portanto,
A
probabilidade de sair uma bola azul ou amarela é: P(AUB) = P(A) + P(B)
P(AUB)
= P(A) + P(B) = 3/15 + 2/15 = 5/15 = 1/3 ≈ 0,33 = 33%
Resposta:
A probabilidade de sair uma bola azul ou amarela é 33%
Ex-11
Alguns amigos estão em uma lanchonete. Sobre a mesa
há duas travessas. Em uma delas há 3 pastéis e 5 coxinhas. Na outra há 2
coxinhas e 4 pastéis. Se ao acaso alguém escolher uma destas travessas e também
ao acaso pegar um dos salgados, qual a probabilidade de se ter pegado um
pastel?
Solução:
A
probabilidade de escolhermos 1 dentre 2 travessas é igual 1/2.
A
probabilidade de escolhermos um pastel na primeira travessa é 3 em 8, ou seja, é 3/8 e como a probabilidade de
escolhermos a primeira travessa é 1/2,
temos:
A
probabilidade de escolhermos um pastel na segunda travessa é 4 em 6, isto é 4/6 e como a probabilidade de
escolhermos a segunda travessa é igual a 1/2,
temos:
Então
a probabilidade de escolhermos um pastel é igual a:
Ex-12
O jogo de dominó é composto de peças retangulares
formadas pela junção de dois quadrados. Em cada quadrado há a indicação de um
número, representado por uma certa quantidade de bolinhas, que variam de
nenhuma a seis. O número total de combinações possíveis é de 28 peças. Se
pegarmos uma peça qualquer, qual a probabilidade dela possuir ao menos um 3 ou
4 na sua face?
Solução:
Chamemos
de A o evento da ocorrência de um 3:
A = { (0, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3) }
Chamemos de B o evento da ocorrência de um 4:
B = { (4, 0), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) }
Veja
que o elemento (4,
3) integra os dois eventos, logo A∩B = {(4, 3)}
Calculando
as probabilidades de A, B e da intersecção, temos:
P(A)
= n(A)/n(S) → P(A) = 7/28
P(B)
= n(B)/n(S) → P(B) = 7/28
P(A∩B)
= n(A∩B)/n(S) → P(A∩B) = 1/28
Finalmente
para o cálculo da probabilidade desejada vamos utilizar a fórmula da probabilidade da união de dois eventos:
Resposta:
A probabilidade de ela possuir ao menos um 3 ou 4 na sua face é 13/28.
Ex-13
Em uma caixa há 4 bolas verdes, 4 azuis, 4 vermelhas
e 4 brancas. Se tirarmos sem reposição 4 bolas desta caixa, uma a uma, qual a
probabilidade de tirarmos nesta ordem bolas nas cores verde, azul, vermelha e
branca?
Solução:
No evento E1 a probabilidade de tirarmos uma bola verde é de 4 em 16:
Como não há
reposição, a cada retirada o número de elementos do espaço amostral diminui em
uma unidade.
No evento E2 a probabilidade de tirarmos uma bola azul é de 4 em 15:
No evento E3 a probabilidade de tirarmos uma bola vermelha é de 4 em 14:
No evento E4 a probabilidade de tirarmos uma bola branca é de 4 em 13:
Finalmente a probabilidade de tirarmos as
bolas conforme as restrições do enunciado são:
Ex-14
Em uma escola de idiomas com 2000 alunos, 500 alunos
fazem o curso de inglês, 300 fazem o curso de espanhol e 200 cursam ambos os
cursos. Selecionando-se um estudante do curso de inglês, qual a probabilidade
dele também estar cursando o curso de espanhol?
Solução:
Chamemos de A o evento que representa o curso de
espanhol e B o evento que representa o curso de
inglês.
Podemos calcular
a probabilidade de ocorrer A tendo ocorrido B através da fórmula:
Conforme o enunciado temos que: n(A∩B) = 200 e n(B) = 500, então:
P(A│B) = n(A∩B)/n(B)
→ P(A│B) = 200/500 → P(A│B) = 2/5
Notamos que no caso da probabilidade
condicional, ao invés de calcularmos a probabilidade em função do número de
elementos do espaço amostral, a calculamos em função do número de elementos do
evento que já ocorreu.
Ex-15
De uma sacola
contendo 15 bolas numeradas de 1
a 15 retira-se uma bola. Qual é a probabilidade desta
bola ser divisível por 3 ou divisível por 4?
Solução:
Vamos
representar por E3 o evento da ocorrência das bolas
divisíveis por 3:
E3 = { 3, 6, 9, 12, 15
}
E por E4 vamos representar o evento da ocorrência
das bolas divisíveis por 4:
E4 = { 4, 8, 12 }
O espaço
amostral é:
S = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }
A
probabilidade de sair uma bola divisível por 3 é:
A
probabilidade de sair uma bola divisível por 4 é:
Como
estamos interessados em uma ocorrência ou em outra, devemos somar as probabilidades, mas como explicado no tópico união de dois eventos, devemos subtrair a probabilidade da
intersecção, pois tais eventos não são mutuamente exclusivos. Como podemos ver,
o número 12 está contido tanto em E3 quanto em E4, ou seja:
A
probabilidade da intersecção é:
Portanto:
Resposta:
A probabilidade da bola ser divisível por 3 ou
divisível por 4 é 7/15.
Ex-16 (VUNESP)
Um baralho tem 100 cartões numerados de 1 a 100. Retira-se 2 cartões ao
acaso (sem reposição). Determine a probabilidade de que a soma dos dois números
dos cartões retirados seja igual a 100.
Solução:
Vamos
determinar o espaço amostral:
Temos
100 cartões que devemos retirar 2 cartões ao acaso, então, temos combinação de
100 cartões 2 a
2.
Seja
A o evento – soma dos 2 cartões é igual a 100.
Portanto,
Resposta:
A probabilidade de que a soma dos dois números dos cartões retirados seja igual a 100 é P(A) = 49/4950.
Ex-17 (FGV-SP)
Uma urna contém 1000 bolinhas numeradas de 1 a 1000. Uma bola é sorteada.
Qual a probabilidade de observarmos um múltiplo de 7?
Solução:
O
espaço amostral é igual a 1000 (=1000 bolinhas).
Seja
A o evento (um múltiplo de 7).
Para
calcular n(A), vamos, por exemplo, aplicar a fórmula geral da PA (progressão
aritmética) onde a1 = 7 (primeiro termo); r = 7 (razão) e am =
inteiro(1000/7)*7 = 994
Resposta:
A probabilidade de observamos um múltiplo de 7 é: P(A) = 71/500
Ex-18 (FUVEST)
Em uma loteria com 30 bilhetes, 4 são premiados. Comprando-se 3
bilhetes, qual a probabilidade de nenhum deles ser premiados?
Solução:
Seja S o
espaço amostral do problema; temos combinação de 30 bilhetes 3 a 3 possibilidades (pois está
comprando 3 bilhetes), no momento da compra, então:
Seja
o evento A: nenhum dos bilhetes é premiado.
Como dos 30 bilhetes 4 são premiados temos que 26 (=30
– 4) não são premiados logo:
Portanto,
a probabilidade de nenhum ser premiado:
Resposta:
A probabilidade de nenhum deles ser premiados é P(A) = 130/203
Ex-19 (MACKENZIE)
Escolhido ao acaso um elemento do conjunto dos divisores positivos
de 30, determine a probabilidade de que ele seja par ou primo.
Solução:
O
espaço amostral S deste problema é:
S={1,2,3,5,6,19,15,30}, logo n(S) = 8
Seja
o evento A: o número par: A={2,6,10,30}, logo n(A) = 4
Portanto,
P(A)
= n(A)/n(S) = 4/8
Agora
seja evento B: o número é primo: B={2,3,5}, logo n(B) = 3
Portanto,
P(B)
= n(B)/n(S) = 3/8
Os
eventos A e B possuem elemento comum: A∩B ={2}, logo n(A∩B) = 1
Portanto,
P(A∩B)=n(A∩B)/n(S) = 1/8
Então
a probabilidade de que ele seja par ou primo é:
P(AUB) = P(A) + P(B) – P(A∩B) = 4/8 + 3/8 – 1/8 = 6/8 = 3/4
P(AUB)
= 3/4 = 0,75 = 75%
Resposta:
A probabilidade de que ele seja par ou primo é 75%.
Ex-20 (UFBA)
Uma fábrica produz 40 peças, das quais seis com defeito. Qual a
probabilidade, escolhendo-se ao acaso uma das peças de que ela seja perfeita?
Solução:
O
espaço amostral S: n(S) = 40
Seja
evento A: Peças perfeitas e seja evento ~A: Peças defeituosas.
Resposta:
A probabilidade de que a peças seja perfeita é 85%.





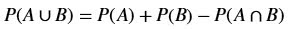










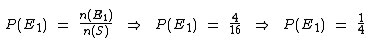








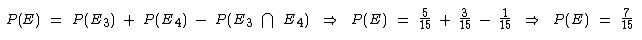



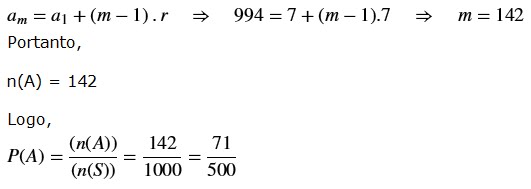




Interessante, gostei de ver, estas probabilidade ajudam bastante,digo obrigado ao site.
ResponderExcluirParabéns pela organização e conteúdo do blog.
ResponderExcluirBoa noite gostei muito os passos de resolução
ResponderExcluirMuito obrigado, gostei muito
ResponderExcluirParabéns!
Uma Urna contém 2 bolas vermelhas e 3 bolas amarelas.Qual a probabilidade de , ao tomar uma bola ao acaso, ela ser amarela?
ResponderExcluirduas cores Evento 5 bolas espaço amostral ... Gostaria que o senhor comentasse por gentileza..
Determinemos o espaço amostral: 5 bolas que a urna possui
ExcluirO número de casos favoráveis é de 3, e nós temos a possibilidade de tirar uma das cinco, então o número de casos possíveis é 5.
P=ncf/ncp
P=3/5
P=0,6
P=60%
Espero ter ajudado
Digo numerador é Evento 2/5 denominador Espaço amostral (total de cores sobre total de bolas objetos observados).
ResponderExcluirMuito obrigado gostei da resolucao das questão
ResponderExcluirAmei
ResponderExcluir