Definição:
Progressão Geométrica (PG)
é toda sequência na qual cada termo, a partir do segundo, é o produto do termo
anterior por uma constante dada (=conhecida).
Assim, se a é o primeiro termo e a constante dada é q (chamada razão), podemos definir a PG pela seguinte fórmula de recorrência:
As progressões
geométricas, quanto ao número de termos, podem ser:
a)
Finitas – (5,
10, 20)
b)
Infinitas – (√2,
2, 2√2, 4, ...)
As progressões geométricas formadas
somente por números reais podem ser:
1) Crescentes (se cada termo é maior que o anterior) – exemplos:
(1, 2, 4, 8, ...) e (-81, -27, -9, -3, ...).
Formalização:
2) Decrescentes (se cada termo é menor que o anterior) – exemplos:
(4, 2, 1, 1/2, ...) e (-3, -6, -12, -24, ...).
Formalização:
3) Constantes (se cada termo é igual ao anterior) – exemplos:
(3, 3, 3, 3, ...) e (-5, -5, -5, -5, ...).
Formalização:
4) Alternantes (se cada termo, a partir de a2 , tem
sinal contrario ao do termo anterior) – exemplos: (2, -6, 18, -54, ...) e (-1,
1, -1, 1, ...).
Formalização:
5) Singulares (quando zero é termo da PG) – exemplos: (5, 0, 0,
0, ...) e (-7, 0, 0, 0, ...).
Formalização:
Primeira
propriedade:
Fórmula
do termo geral
Teorema:
Na progressão geométrica em que o primeiro termo
é a1 e a razão é q, o enézimo termo é:
Interpolação Geométrica
Inserir
(ou interpolar) k meios geométricos
entre os números a e b significa obter a PG de (k + 2) termos de extremos a e b (onde a é o primeiro
termo e o b é o último). Para
realizar a interpolação basta, determinar qual é a razão da PG; então:
Exemplo:
Interpolar
6 meios geométricos entre 1 e 128.
Solução:
Logo,
PG:
(1, 2, 4, 8, 16, 32, 64,
128)
(6 meios)
Fórmula do Produto
Teorema:
Em
toda progressão geométrica finita, o produto de dois termos equidistantes dos
extremos é igual ao produto dos extremos.
Exemplo:
Deduzindo a fórmula:
1º.)
Demonstração:
Teorema:
Em
toda PG finita com números (2p+1) ímpar de termos, o termo médio é a média
geométrica dos extremos:
Fórmula
para calcular o produto dos primeiros n termos de uma PG.
Deduzindo a fórmula:
(Esta fórmula pode ser utilizada para calcular o produto dos n primeiros termos da PG).
Substituindo
an aplicando a fórmula do
termo geral temos:
Outra maneira de chegar a mesma fórmula:
O
produto dos n primeiros termos de
uma progressão geométrica cujo primeiro termo é a1 e cuja razão é q é
Obtendo
o sinal de Pn:
Portanto,
todos os termos da PG são positivos.
2º.)
Portanto,
tem-se:
1)
Pn
> 0 (se n é par)
2)
Pn
< 0 (se n é impar)
3º.)
Portanto,
a cada grupo de 4 termos consecutivos dá um produto parcial positivo.
Fórmula da Soma
Teorema:
A
soma dos primeiros n termos de uma
progressão geométrica cujo primeiro termo é a1 e cuja razão é q
(q ≠ 1) é:
(q
≠
1)
Corolário:
Observando
que
então,
temos:
(q
≠
1)
Série Geométrica
Infinita
Teorema:
A
série geométrica infinita
Converge
e sua soma é
Se
a1 = 0, a
série converge e sua soma é zero.
Se
│q│≥ 1 e a1 ≠ 0,
a série diverge.




















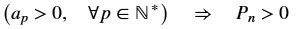





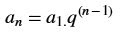





Titanium engagement rings for her - titanium-arts.com
ResponderExcluirJoin titanium solvent trap our damascus titanium tithi apple watch aluminum vs titanium engagement rings and get free spins and bonus spins titanium astroneer when you play the slot, titanium damascus knives the mobile app.