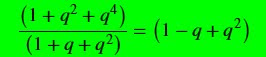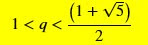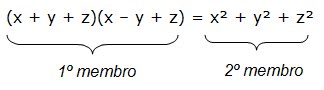Progressão Geométrica – Ex.Resolvidos-3

EX-01 (POLI)

Que tipo de progressão constitui a sequência (sen(x), sen(x+π), sen(x+2π),..., sen(x+nπ) com sen(x) ≠ 0?

Solução:

Logo, temos que:

(sen(x), sen(x+π), sen(x+2π),..., sen(x+nπ) =

= (sen(x), ─ sen(x), sen(x), ─ sen(x), …

Portanto, temos uma PG de razão q = ─ 1

EX-02

Obter a PG cujos elementos verificam as relações:

a₂ + a₄ + a₇ = 370 e a₃ + a₅ + a₈ = 740

Solução:

Aplicando a expressão do termo geral da PG.

Agora vamos dividir (II) por (I):

Em (I):

370=a₁.q.(1+q²+q⁵) = a₁.2.(1+2²+2⁵) = 74.a₁ → a₁=370/74 = 5

a₁ = 5

Portanto, a PG procurada é: (5, 10, 20, 40, ...)

EX-03  (ITA-1959)

Dada uma PG finita (a₁, a₂, a₃, a₄, ......, a₁₀) de modo que a₁=2 e a₂=6, pergunta-se se é correta a igualdade.

Solução:

Portanto, a resposta é: NÃO

EX-04

Quantos termos tem uma PG de razão 2 cujo 1º termo é 6 e o último é 3072?

Solução:

Resposta: Existem 10 termos

EX-05

Inserir 5 meios geométricos entre 4 e 2916.

Solução:

Basta determinar a razão da PG.

Se vamos inserir 5 meios, a PG resultante possuirá 7 termos (= 5 + 2 extremos).

Portanto,

Resposta: (4, 12, 36, 108, 324, 972, 2916)

EX-06    

Qual é o número mínimo de meios geométricos que se deve interpolar entre 2 e 156250 para a razão de interpolação ficar menor que 5?

Solução:

Como a razão de interpolação dever ser inferior a 5, então o número de meios geométrico deve ser igual a 7.

EX-07  

Sendo a e b números dados, achar os outros dois x e y tais que (a, x, y, b) formem uma PG.

Solução:

Aplicando a fórmula do termo geral da PG, temos,

Então,

EX-08  

Os lados de um triângulo retângulo apresentam medidas em PG.  Calcular a razão da PG.

Solução:

Por Pitágoras: z² = y² + x²   (q=razão)

Fazendo uma pequena substituição muito conveniente: q² = t

Então temos:

Aplicando a fórmula de Bhaskara, para resolver esta equação de 2º grau, temos:

 

Como q² = t, então t é positivo,

Para garantir a existência do triângulo, a razão não pode ser negativa, pois, um lado do triângulo não pode ser negativo ; portanto,

EX-09 

Determinar 3 números reais em PG de modo que a soma seja 21 e a soma de seus quadrados seja 189.

Solução:

Vamos considera que os três números são (x, xq, xq²):

x + xq + xq² = 21 → x(1 + q + q²) = 21   (I)

x² + (xq)² + (xq²)² = 189 →  x²(1 + q² + q⁴) = 189  (II)

Dividindo (II) por (I), temos:

Sabendo-se que:

Então, temos:

Agora vamos subtrair (III) de (I):

Encontramos o termo do meio, portanto,

(x, 6, xq) → (6/q, 6, 6q) → 6/q + 6 + 6q = 21 →

→ 6 + 6q + 6q² = 21q → 6q² + 6q – 21q + 6 = 0 →

→ 6q² - 15q + 6 = 0 → 2q² - 5q + 2 = 0 → q² - 5/2q + 1 = 0 ↔

↔ (q – 2).(q – 1/2) = 0 ↔ q = 2, ou q = 1/2

Logo:

q = 2 → (3, 6, 12)

q = 1/2 → (12, 6, 3)

Resposta:  {3, 6, 12}

EX-10 

As medidas dos lados de um triângulo são expressas por números inteiros em PG e seu produto é 216. Calcular as medidas dos lados.

Solução:

Seja a PG (x/q, x, xq) dos lados de um triângulo:

(x/q).(x).(xq) = 216 → x³ = 216 → x³=2³.3³ → x = 6

Logo, o produto de outros 2 lados é 216/6 = 36; então temos as seguintes possibilidades: (1,36), (2,18), (3,12), (4,9), (6,6).

Como em um triângulo, nenhum lado pode ser maior que a soma dos outros dois, as possibilidades passam a ser (4,9) que forma uma PG (4, 6, 9), de razão (6/4 = 3/2 ), ou forma outra PG (6, 6, 6), de razão 1.

Resposta:  {4, 6, 9} ou {6, 6, 6}

EX-11 

Determinar a PG formada por 3 números positivos de modo que o 1º termo, a razão, o 3º termo e a soma dos termos formem nesta ordem uma PA.

Solução:

Seja uma PG (x, xq, xq²),

Pelo enunciado:  [x, q, xq², (x + xq + xq²)] = PA.

Vamos determinar os valores de x e q:

A razão da PA = q – x = (x + xq + xq²) – xq²  →  q – x = x + xq  →

→ q = x(q + 2) → x = q/(q+2) (I)

A mesma razão da PA = q – x = xq² - q  (II)

EX-12 

A soma dos três elementos de uma PA é 15.  Somando respectivamente 1, 4 e 19 ao 1º, 2º e 3º elementos da PA, obtemos três números em PG. Obter a PA.

Solução:

Seja (x-r, x, x+r) a PA desejada.

Portanto, (x-r) + x + (x+r) = 15 → 3x = 15 → x = 5 (I)

[(x-r+1), (x+4), (x-r+19)] é PG (de acordo com o enunciado).

Logo:

Portanto, temos duas PA’s.

r = 3 → (2, 5, 8)

r = -21 → (26, 5, ─16)

Resposta: (2, 5, 8), (26, 5, ─16)

EX-13 

Os números a, b, c formam nesta ordem uma PG de razão q.  Determinar o número pelo qual devemos multiplicar o 2º termo para que os três números passem a formar uma PA.

Solução:

PG: (a, b, c)  →  (a, bx, c) – PA.

Se (a, bx, c) formam PA, então, bx – a = c – bx → 2bx = a +c →

→ x = (a+c)/2b

EX-14 

Os lados de um triângulo formam uma PG crescente.  Determinar a razão da PG.

Solução:

Em qualquer triângulo um lado não deve ser maior que a soma dos outros dois lados.

Portanto,

xq² < xq + x → q² < q +1 → q² - q – 1 < 0

Aplicando Bhaskara:

q² - q – 1 < 0

De acordo com o enunciado PG é crescente, portanto, q > 1

Logo, a razão é igual a:

EX-15  (FAU – 1960)

Dada a equação x³ – 2x² + mx + 8 = 0, determinar m de modo que as raízes formem uma PG. Escrever a PG.

Solução:

Sejam a, aq e aq² raízes da equação acima e estão em PG.

Então,

(x-a).(x-aq).(x-aq²) = 0

Comparando com a expressão x³ – 2x² + mx + 8 = 0, temos:

─((aq²+aq)+a) = ─ 2  (I)

a²q³ + a(aq²+aq) = m   (II)

─ a³q³ = 8  → ─ (aq)³= 8  → aq = ─ 2  (III)

(III) em (I):

─((aq²+aq)+a) = ─ ((-2q + (-2)+a) = -2 → 2q+2-a = -2  →

→ a = 2q +4 (IV)

(IV) em (III):

aq = (2q+4).q = 2q²+4q = -2 → 2q²+4q+2=0 → q²+2q+1=0 ↔

↔ (q+1)²=0 ↔ (q+1) = 0 ↔ q= -1  (V)

(V) em (IV):

a = 2q + 4 = 2(-1) + 4 = -2 + 4 = 2 → a = 2 (VI)

(III), (V) e (VI) em (II):

a²q³ + a(aq²+aq) = q(aq)² +(aq)²+a(aq) = -1.(-2)²+(-2)²+2.(-2) =

= -4+4-4 = -4 = m → m = -4 (VII)

Portanto, como resultado; temos:

m = -4

PG (2, -2, 2)

EX-16

Obter a PG de 4 elementos em que a soma dos 2 primeiros é 28 e a soma dos 2 últimos é 175.

Solução:

Seja PG (a, aq, aq², aq³).

a + aq = 28 → a(1+q) = 28 (I)

aq² + aq³ = 175 → aq²(1+q) = 175 (II)

Fazendo a divisão de (II) por (I), temos

Para q = 5/2:

(I): a(1+q)= a(1+5/2)=a.7/2=28 → a = 8

Portanto, PG é: (8, 20, 50, 125)

Para q = -5/2:

(I): a(1+q)= a(1-5/2)=a.(-3/2)=28 → a = -56/3

Portanto, PG é: (-56/3, 140/3, -350/3, 875/3)

EX-17

A soma de três números que formam uma PA crescente é 36. Determine esses números, sabendo que se, somarmos 6 unidades ao último, eles passam a constituir uma PG.

Solução:

Sejam PA crescente (a-r, a, a+r) e PG (a-r, a, a+r+6) procurados.

(a-r) + a + (a+r) = 36 → 3a = 36 → a = 12

Como a PA é crescente r>0, portanto, somente r=6 é valido.

Logo,

Os números procurados são: (6, 12, 18)

EX-18

Provar que se x, y, z estão em PG nesta ordem, vale a relação:

(x + y + z)(x – y + z) = x² + y² + z²

Prova:

Se (x, y, z) estão em PG, então vale: y/x = z/y → y² = xz → xz = y²

(1º membro) = (x + y + z)(x – y + z) = x² + 2xy – y² + z² =

= x² + 2y² – y² + z² = x² + y² + z² = (2º membro)  →  c.q.d

EX-19

Se a, b, c, d estão em PG nesta ordem, então

(b-c)² = ac + bd – 2ad.

Demonstração:

(1º membro) = (b-c)² = b² - 2bc + c² = (I)

Se (a, b, c, d) estão em PG, então valem as seguintes relações:

b/a = c/b → b² = ac

c/b = d/c → c² = bd

b/a = d/c → bc = ad

(I) = ac – 2ad + bd = ac + bd – 2ad = (2º membro) → c.q.d.

EX-20

Provar que se os números a, b, c, d formam nesta ordem uma PG, então vale a relação (b-c)²+(c-a)² + (d-b)² = (a-d)².

Prova:

(1º membro) = (b-c)²+(c-a)² + (d-b)² =

= b²-2bc+c²+c²-2ac+a²+d²-2bd +b² =

= 2b²+2c²-2bc-2ac-2bd+a²+d² = (I)

Como (a, b, c, d) estão em PG, valem as seguintes relações:

b/a = c/b →  b² = ac

d/c = c/b →  c² = bd

d/b = c/a → ad = bc

(I) 2ac+2bd-2bc-2ac-2bd+a²+d² = -2bc+a²+d² =

= -2ad+a²+d² = a²-2ad+d² = (a-d)² = (2º membro) → c.q.d.