EX-01 (FUVEST 2000)
Um
investidor quer aplicar 120 mil reais. Seu corretor lhe oferece um
investimento, em duas fases, com as seguintes regras:
- Na 1ª fase do
investimento, ocorrerá um dentre os dois eventos seguintes: com
probabilidade p, o investidor ganha metade do que investiu; com
probabilidade (1-p), o investidor perde um terço do que investiu.
- Na 2ª fase do
investimento, a quantia final da 1ª fase será reinvestida, de forma
independente da 1ª fase. Neste novo investimento, ocorrerá um dentre os
dois eventos seguintes: com probabilidade 1/2, o investidor ganha a quarta
parte do que foi reinvestido; com probabilidade 1/2, o investidor perde
metade do que foi reinvestido.
a) Se o investidor aplicar seu dinheiro desta forma, com que valores pode
ficar ao término do investimento? Qual a probabilidade, em função de p, de
ficar com cada um desses valores?
b) Uma revista especializada informa que, neste investimento, a
probabilidade de perder dinheiro é 70%. Admitindo como correta a informação da
revista, calcule p.
Solução:
Fazendo a árvore de possibilidades, temos:
Obs.: A segunda fase é independente da primeira
fase, portanto, permite colocar 1/2 e 1/2 diretamente. Os eventos A (=1ª fase) e B (=2ª fase) são
independentes entre si; logo:
Respostas:
a) O investidor pode ficar com as seguintes
situações:
1) R$ 225 000,00 [1/2*p]
2) R$ 90
000,00 [1/2*p]
3) R$ 100 000,00 [1/2*(1-p)]
4) R$ 40
000,00 [1/2*(1-p)]
b) Analisando as 4 possibilidades, o investidor só
não perde na 1ª possibilidade. Como, conforme a revista, a probabilidade de
perder é de 70%; logo a probabilidade de não perder é de 30% (que é
complementar):
Outra maneira de resolver o item b.
A probabilidade de perder é igual a:
EX-02 (FUVEST 2001)
Um dado, cujas faces estão
numeradas de um a seis, é dito perfeito se cada uma das seis faces tem
probabilidade 1/6 de ocorrer em um lançamento. Considere o experimento que
consiste em três lançamentos independentes de um dado perfeito. Calcule a
probabilidade de que o produto desses três números seja
a) par;
b) múltiplo de 10.
Solução:
a) Para que o produto seja par, basta que um dos fatores seja par. E para
que o produto seja ímpar é preciso que os três números sejam ímpares.
Então, vamos calcular a
probabilidade do produto seja par, aplicando o conceito de probabilidade
complementar:
p(produto par) = 1 - p(produto ímpar)
Logo, a probabilidade do
produto ser par é:
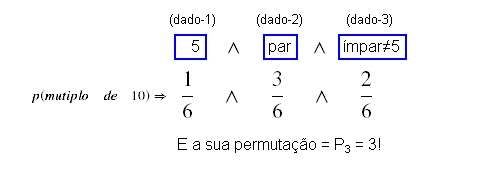
b) Para termos um produto que seja múltiplo de 10, basta
ter, no mínimo, um 5 com um número par
Então, temos as seguintes
possibilidades:
1) Primeira possibilidade,
(probabilidade p1):
2) Segunda possibilidade,
(probabilidade p2):
3) Terceira possibilidade,
(probabilidade p3):
Portanto, p(múltiplo de
10) = p1 + p2 + p3
Portanto,
EX-03 (FUVEST 2002)
Um tabuleiro tem 4 linhas
e 4 colunas. O objetivo de um jogo é levar uma peça da casa inferior esquerda
(casa (1,1)) para a casa superior direita (casa (4,4)), sendo que esta peça
deve mover-se, de cada vez, para a casa imediatamente acima ou imediatamente à
direita. Se apenas uma destas casas
existir, a peça irá mover-se necessariamente para ela. Por exemplo, dois
caminhos possíveis para completar o trajeto são: (1,1)→(1,2)→(2,2)→(2,3)→(3,3)→(3,4)→(4,4) e (1,1)→(2,1)→(2,2)→(3,2)→(4,2)→(4,3)→(4,4).
a)
Por quantos caminhos distintos pode-se completar esse trajeto?
b) Suponha que o caminho a
ser percorrido seja escolhido da seguinte forma: sempre que houver duas opções
de movimento, lança-se uma moeda não viciada; se der cara, a peça move-se para
a casa da direita e se der coroa, ela se move para a casa acima. Desta forma,
cada caminho contado no item a) terá uma certa probabilidade de ser percorrido.
Descreva os caminhos que tem maior probabilidade de serem percorridos e calcule
essa probabilidade.
Solução:
a)
Podemos observar na figura
que: Qualquer caminho da casa (1,1) à casa (4,4) pode ser descrito por uma
sequência de três “X” e três “Y”. Da
mesma forma, qualquer permutação da sequencia XXXYYY vai corresponder a um
caminho válido da casa (1,1) à casa (4,4).
Portanto, o número de
caminhos distintos de casa (1,1) à casa (4,4) é igual ao número de permutações
de XXXYYY:
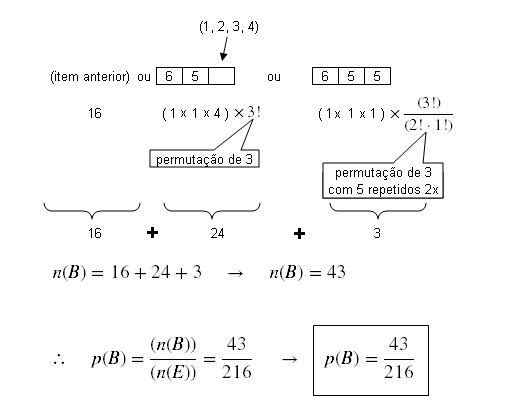
b)
A probabilidade de percorrer
um caminho onde ocorra n lançamentos da moeda é:
Portanto, um caminho que
envolva menos lançamentos de dados possui maior probabilidade de ser
percorrido. A figura desenhada, mostra
que os caminhos através de casas na borda superior e da borda direita (onde não
se lança a moeda) são os (caminhos) que vão possui a maior probabilidade. E
esses caminhos correspondem às sequências: XXXYYY e YYYXXX e cada um com
probabilidade igual a:
EX-04 (FUVEST 2003)
Em uma equipe de basquete,
a distribuição de idades dos seus jogadores é a seguinte:
Será sorteada,
aleatoriamente, uma comissão de dois jogadores que representará a equipe junto
aos dirigentes.
a) Quantas possibilidades
distintas existem para formar esta comissão?
b) Qual a probabilidade da
média de idade dos dois jogadores da comissão sorteada ser estritamente menor
que a média de idade de todos os jogadores?
Solução:
a) Número total de
jogadores é igual a 12, portanto, podemos ter combinação de 12, 2 a 2 possíveis comissões:
b) A média de todos os
jogadores é:
Sejam A e B as idades dos
2 jogadores e vamos considerar que A≥B.
Logo, a média dessas
idades é menor que a média das idades de
todos os jogadores se, somente se,
1) Ambos os jogadores
possuem menos de 27 anos; ou
2) Um dos jogadores possui
29 anos, por exemplo, A=29; ou
3) Um dos jogadores possui
31 anos, por exemplo, A=31; ou
4) Um dos jogadores possui
32 anos, por exemplo, A=32.
Portanto,
1) A<27 ˄ B<27, então A+B<54,
Assim, pela tabela,
tem-se: 1 jogador de 22 anos, 3 jogadores de 25 anos e 4 jogadores de 26 anos. Logo, temos 1+3+4=8 jogadores.
2) A=29
Logo, devemos ter:
A+B<54 ↔ 29+B<54 ↔ B<25.
Assim, pela tabela, temos:
B=22 anos.
Portanto, há apenas 1
maneira de escolher 2 jogadores
3) A=31 (tem 2 jogadores
com 31 anos)
Neste caso tem-se:
A+B<54 ↔ 31+B<54 ↔ B<23
Pela tabela, temos: B=22 anos.
Portanto, há apenas 2
maneiras de escolher 2 jogadores
4) A=32
Para este caso tem-se: A+B<54
↔ 32+B<54 ↔ B<22
O que é impossível.
Portanto, não há maneira
de escolher 2 jogadores.
EX-05 (FUVEST 2005)
Uma pessoa dispõe de um
dado honesto, que é lançado sucessivamente quatro vezes. Determine a probabilidade de que nenhum dos
números sorteados nos dois primeiros lançamentos coincida com algum dos números
sorteados nos dois últimos lançamentos.
Solução:
São 4 lançamentos →
Espaço Amostral é: 6*6*6*6=64 →
n(E) = 1296
Sejam
X = evento – 2 primeiros
lançamentos resultam em números iguais e
Y = evento – 2 primeiros
lançamentos resultam em números diferentes.
Então, a probabilidade de que nenhum dos números sorteados
nos 2 primeiros lançamentos coincida com algum dos números sorteados nos 2
últimos lançamentos é:
EX-06 (FUVEST 2007)
Uma urna contém 5 bolas
brancas e 3 bolas pretas. Três bolas são retiradas ao acaso, sucessivamente,
sem reposição. Determine
a) a probabilidade de que
tenham sido retiradas 2 bolas pretas e 1 bola branca.
b) a probabilidade de que
tenham sido retiradas 2 bolas pretas e 1 bola branca, sabendo-se que as três
bolas retiradas não são da mesma cor.
Solução:
O número de maneiras de
retirar 3 bolas de uma urna contendo 8 bolas é:
Portanto, o espaço
amostral é igual a: n(E)=56
a) Seja A o evento:
retirar 2 bolas pretas e 1 bola branca da urna que contém 5 bolas brancas e 3
bolas pretas.
Então,
Logo, a probabilidade de
que tenha sido retiradas 2 bolas pretas e 1 bola branca é:
b) “Sabendo-se que as três
bolas retiradas não são da mesma cor”, isto é, não seja BBB, ou PPP.
Então,
Já
temos que n(A)=15, sendo A o evento de retirar 2 bolas pretas e 1bola branca.
Então,
a probabilidade de ocorrência de A é:
EX-07 (FUVEST 2008)
Em um jogo entre Pedro e
José, cada um deles lança, em cada rodada, um mesmo dado honesto uma única vez.
O dado é cúbico, e cada uma de suas 6 faces estampa um único algarismo de
maneira que todos os algarismos de 1
a 6 estejam representados nas faces do dado.
Um participante vence, em
uma certa rodada, se a diferença entre seus pontos e os pontos de seu
adversário for, no mínimo, de duas unidades. Se nenhum dos participantes
vencer, passa-se a uma nova rodada. Dessa forma, determine a probabilidade de
a) Pedro vencer na
primeira rodada;
b) nenhum dos dois
participantes vencer na primeira rodada;
c) um dos participantes
vencer até a quarta rodada.
Solução:
Da figura:
1. Seja E o conjunto de
todos os possíveis resultados de cada rodada, então o campo amostral é: n(E) = 36
2. Seja A o conjunto de
todos os possíveis resultados com diferença entre os pontos serem, no mínimo,
de 2 unidades, então tem-se: n(A) = 20.
3.Seja B o conjunto de
todos os possíveis resultados com diferença inferior a 2 unidades, então
tem-se: n(B) = 16
4.Seja P o conjunto de
possíveis resultados que o Pedro vence na primeira rodada:
P = {(3,1), (4,1), (4,2),
(5,1), (5,2), (5,3), (6,1), (6,2), (6,3), (6,4)}
Logo, n(P) = 10
a) A probabilidade de
Pedro vencer na primeira rodada é:
b) A probabilidade de não
haver vencedor na primeira rodada é:
c) Se a probabilidade de
não haver vencedor na primeira rodada é: p’=4/9, então, a probabilidade de
haver vencedor é p’’=1- 4/9 = 5/9.
Portanto, a probabilidade
de a disputa ser vencida na
1- primeira rodada = 5/9;
2 - segunda rodada =
4/9*5/9 = 20/81;
3 - terceira rodada =
4/9*4/9*5/9 = 80/729;
4 – quarta rodada =
4/9*4/9*4/9*5/9 = 320/6561
Logo, a probabilidade de
um dos participantes vencer até a quarta rodada é:
EX-08 (FUVEST 2009)
Um apreciador deseja
adquirir, para sua adega, 10 garrafas de vinho de um lote constituído por 4
garrafas da Espanha, 5 garrafas da Itália e 6 garrafas da França, todas de
diferentes marcas.
a) De quantas maneiras é
possível escolher 10 garrafas desse lote?
b) De quantas maneiras é
possível escolher 10 garrafas do lote, sendo 2 garrafas da Espanha, 4 da Itália
e 4 da França?
c) Qual é a probabilidade
de que, escolhidas ao acaso, 10 garrafas do lote, haja exatamente 4 garrafas a
Itália e, pelo menos, uma garrafa de cada um dos outros dois países?
Solução:
a) O número de maneiras de
escolher 10 garrafas do lote é:
Portanto, são possíveis
3003 maneiras
b) Escolher 10 garrafas
aleatoriamente da seguinte maneira: 2 espanhol e 4 italiano e 4 francês.
Então, o número de
maneiras possíveis é:
Portanto, são possíveis
450 maneiras
c)
Calculando todas as
possibilidades, temos:
Portanto,
a probabilidade pedida é:
EX-09 (FUVEST 2010)
Seja um número inteiro, n≥0.
a) Calcule de quantas
maneiras distintas n bolas idênticas podem ser distribuídas entre Pedro e Luís.
b) Calcule de quantas
maneiras distintas n bolas idênticas podem se distribuídas entre Pedro, Luís e
Antônio.
c) Considere, agora, um
número natural k tal que 0≤k≤n. Supondo que cada uma das distribuições do item
b) tenha a mesma chance de ocorrer, determine a probabilidade de que, após uma
dada distribuição, Pedro receba uma quantidade de bolas maior ou igual a k.
Solução:
Sabendo-se que o número de
soluções inteiros não negativas da equação linear com coeficientes unitários é:
Equação:
Número de soluções:
a) Calcular
de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre
Luís (L) e Antônio (A) é mesma coisa que calcular o número de soluções da
equação
Onde xL e xA
são as quantidades não-negativas de bolas ganhas e, respectivamente, pelo
Luís e Antônio.
Então, o número de
soluções inteiros não negativas da equação (1) é:
b) Adicionando o Pedro
(P), temos a seguinte equação:
Então o número de soluções
inteiras não negativas é dado por:
c) k ϵ N
e 0 ≤ k ≤ n e k ≥ xp
Então podemos escrever que
yp = xp – k, sendo yp é a quantidades de bolas
a mais que k (bolas) que o Pedro ganhou.
De (2):
Portanto, o número de
soluções inteiras não negativas é:
Logo, a probabilidade
procurada é:
EX-10 (FUVEST 2011)
Para a prova de um
concurso vestibular, oram elaboradas 14 questões, sendo 7 de Português, 4 de
Geografia e 3 de Matemática. Diferentes versões da prova poderão ser
produzidas, permutando-se livremente essas 14 questões.
a) Quantas versões
distintas da prova poderão ser produzidas?
b) A instituição
responsável pelo vestibular definiu as versões classe A da prova como sendo aquelas
que seguem o seguinte padrão: as 7 primeiras questões são de Português, a
última deve ser uma questão de Matemática e, ainda mais: duas questões de
Matemática não podem aparecer em posições consecutivas. Quantas versões classe A distintas da prova
poderão ser produzidas?
c) Dado que um candidato
vai receber uma prova que começa com 7 questões de Português, qual é a probabilidade de que ele receba uma
versão classe A?
Solução:
a) Podemos permutar de 14!
Maneiras diferentes.
Portanto, temos 14! Versões distintas de prova.
b)
c)
EX-11 (FUVEST 2012)
a) Dez meninas e seis
meninos participarão de um torneio de tênis infantil. De quantas maneiras
distintas essas 16 crianças podem ser separadas nos grupos A, B, C e D, cada um
deles com 4 jogadores, sabendo que os grupos A e C serão formados apenas por
meninas e o grupo B, apenas por meninos?
b) Acontecida a fase
inicial do torneio, a fase semifinal terá os jogos entre Maria e João e entre
Marta e José. Os vencedores de cada um dos jogos farão a final. Dado que a
probabilidade de um menino ganhar de uma menina é 3/5, calcule a probabilidade
de uma menina vencer o torneio.
Solução:
b) São possíveis 2
possibilidades da disputa de final:
Pelo enunciado as
semifinais são entre Maria x João e Marta x José:
1- As duas meninas ganham
as semifinais:
2 – Ou, 1 menina e 1
menino são vencedores das semifinais:
Portanto, a probabilidade
de menina ganhar o torneio é:
EX-12 (FUVEST 2013)
Sócrates e Xantipa
enfrentam-se em um popular jogo de tabuleiro, que envolve a conquista e
ocupação de territórios em um mapa. Sócrates ataca jogando três dados e Xantipa
se defende com dois. Depois de lançados os dados, que são honestos, Sócrates
terá conquistado um território se e somente se as duas condições seguintes
forem satisfeitas.
1) o maior valor obtido em
seus dados for maior que o maior valor obtido por Xantipa.
2) algum outro dado de
Sócrates cair com um valor maior que o menor valor obtido por Xantipa.
a) No caso em que Xantipa
tira 5 e 5, qual á a probabilidade de Sócrates conquistar o território em jogo?
b) No caso em que Xantipa
tira 5 e 4, qual é a probabilidade de Sócrates conquistar o território em jogo?
Solução:
a) XANTIPA tira 5 e 5,
então SÓCRATES deve obter pelo menos 2 seis:
b) XANTIPA tira 5 e 4,
então SÓCRATES deve obter pelo menos 2 seis (item anterior), ou um único 6 e
pelo menos um 5.
EX-13 (FUVEST 2014)
Um recipiente
hermeticamente fechado e opaco contém bolas azuis e bolas brancas. As bolas de
mesma cor são idênticas entre si e há pelo menos uma de cada cor no recipiente.
Na tentativa de descobrir quantas bolas de cada cor estão no recipiente,
usou-se uma balança de dois pratos. Verificou-se que o recipiente com as bolas
pode ser equilibrado por:
(i) 16 bolas brancas
idênticas as que estão no recipiente ou
(ii) 10 bolas brancas e 5
bolas azuis igualmente idênticas as que estão no recipiente ou
(iii) 4 recipientes vazios
também idênticos ao que contém as bolas.
Sendo PA, PB
e PR, respectivamente, os pesos de uma bola azul, de uma bola branca
e do recipiente na mesma unidade de medida, determine
(a) os quociente PA/PB
e PR/PB;
(b) o número nA
de bolas azuis e o número nB de bolas brancas no recipiente.
Solução:
Fazendo o desenho com as
informações fornecidas, para melhor visualização:
Então, temos as seguintes
igualdades:
a)
b)
Então, para k um número
inteiro positivo podemos escrever que:
EX-14 (FUVEST 2015)
Um “alfabeto minimalista”
é constituído por apenas dois símbolos, representados por * e #. Uma palavra de
comprimento n, n≥1, é formada por n escolhas sucessivas de um desses
dois símbolos. Por exemplo, # é uma palavra de comprimento 1 e #**# é uma
palavra de comprimento 4.
(a) quantas palavras de
comprimento menor do que 6 podem ser formadas?
(b) qual é o menor valor
de n para o qual é possível formar 1.000.000 de palavras de tamanho menor ou
igual a n?
Solução:
a) As palavras com
comprimento menor que 6, podem ter 1, 2, 3, 4 e 5 caracteres:
b)
Menor N para formar
1.000.000 palavras de tamanho menor ou igual a N.
Logo, temos:
EX-15 (FUVEST 2016)
João e Maria jogam dados
em uma mesa. São cinco dados em forma de poliedros regulares: um tetraedro, um
cubo, um octaedro, um dodecaedro e um icosaedro. As faces são numeradas de 1 a 4 no tetraedro, de 1 a 6 no cubo, etc. Os dados
são honestos, ou seja, para cada um deles, a probabilidade de qualquer uma das
faces ficar em contato com a mesa, após o repouso do dado, é a mesma. Num
primeiro jogo, Maria sorteia, ao acaso, um dos cinco dados, João lança e
verifica o número da face que ficou em contato com a mesa.
a) Qual é a probabilidade
de que esse número seja maior do que 12?
b) Qual é a probabilidade
de que esse número seja menor do que 5?
Num segundo jogo, João
sorteia, ao acaso, dois dos cinco dados. Maria os lança e anota o valor da soma
dos números das duas faces que ficaram em contato com a mesa, após o repouso
dos dados.
c) Qual é a probabilidade
de que esse valor seja maior do que 30?
Solução:
a)
Para que o resultado seja
maior que 12, o dado escolhido deve ser icosaedro.
A probabilidade de
escolher o icosaedro é 1/5.
A probabilidade de tirar
número maior que 12, [13, 14, 15, 16, 17, 18, 19, 20], é 8/20.
Portanto, a probabilidade
pedida é:
b)
As probabilidades de que o
número seja menor que 5, em cada dado é conforme a tabela a seguir:
E a probabilidade de
escolher um dos dados é 1/5.
Portanto, a probabilidade
procurada é dada por:
c)
Para que a soma do números
seja maior que 30, os dados escolhidos deverão ser o icosaedro e dodecaedro.
A probabilidade de que
esses dados sejam escolhidos é:
Ou podemos pensar da
seguinte forma também:
(João sorteou o icosaedro
e dodecaedro, simultaneamente)
Os pares de resultados
cuja soma é maior que 30 são:
Logo, com essas
informações, a probabilidade de a soma seja maior que 30 é:
Portanto, a probabilidade
procurada é:















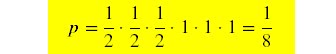










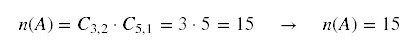
















































Nenhum comentário:
Postar um comentário